[数据结构]-二叉树的常见问题的递归算法

发表于 | 分类于 | 阅读次数

求二叉树的节点数

递归子问题：二叉树的节点数等于根+左子树的节点数+右子树的节点数。

递归终止条件：root == null，即该子树已经遍历结束

1
2
3
4
5
6
public int nodeCount(biNode root){
    if (root == null)
        return 0;
    return nodeCount(root.left)+nodeCount(root.right)+1;

}

求二叉树的深度

递归子问题：二叉树的深度等于max(根+左子树深度，根+右子树深度）

递归终止条件：root == null，即分支已经遍历结束

1
2
3
4
5
public int depthTree (biNode root){
     if (root == null)
         return 0;
     return Math.max(depthTree(root.left)+1, depthTree(root.right)+1);
 }


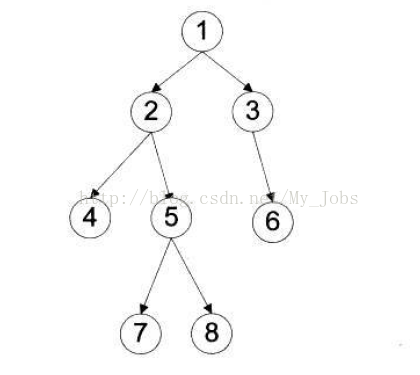
depth = max(max(3, max(4, 4)), max(3))

求二叉树叶子数目

递归子问题：二叉树的深度等于左子树的叶子数+右子树的叶子数

递归终止条件：

  • root == null，该节点不是叶子，数量为0
  • root.right==null&& root.left==null，该节点没有孩子，是一个叶子，数量为1
1
2
3
4
5
6
7
public int leavesCount (biNode root){
    if (root == null)
        return 0;
    if (root.right==null&& root.left==null)
        return 1;
    return leavesCount(root.left)+leavesCount(root.right);
}

判断两棵树的结构是否相同

递归子问题：当两棵树的左子树和右子树的结构都想同时，两棵树结构相同

递归终止条件：

  • (root1!=null&&root2==null)||(root1==null&&root2!=null)，存在一个父节点，他们的孩子在两棵树中结构不同，返回false
  • root1==null&&root2==null，遍历完成，没有出现结构不同的情况，返回true
1
2
3
4
5
6
7
8
public static boolean isEqual(biNode root1, biNode root2){
    if ((root1!=null&&root2==null)||(root1==null&&root2!=null)){
        return false;
    }
    if (root1==null&&root2==null)
        return true;
    return isEqual(root1.left, root2.left) && isEqual(root1.right, root2.right);
}

求第k层节点数

k>0,第0层是跟节点

递归子问题：第k层节点数=根的左子树的第k-1层节点数 + 根的右子树的第k-1层节点数

递归终止条件：

  • root == null，这一层没有节点，返回0
  • k == 0，第k层有节点
1
2
3
4
5
6
7
8
9
public int kNodesCount (biNode root, int k){
    if(root == null){  //k<0是非法输入，root == null说明第k层没有节点 0
        return 0;
    }
    if (k == 0){  //k ==0 且该层有节点说明这个第k层的一个节点
        return 1;
    }
    return kNodesCount(root.left, k-1)+kNodesCount(root.right,k-1);
}

递归思想理解

递归就是将一个大规模的问题用一个可以解决小规模输入子问题来解决。要找到解决问题的子问题是递归思想的关键，将大问题拆成子问题，由大到小，由近及远，小（远）到什么程度由终止条件控制。当我们把问题“递”到足够小（远），开始“归”，将所有返回值进行处理的到最终大规模问题的解。

将递归问题理解成“递”和“归”两个阶段。